Betting Systems
The Truth Behind Betting Systems
Casino players will always search for more innovative strategies and betting systems that they can use to guarantee profits. In the long run, it’s all about beating the casino. Over the years, some of these betting systems have been found to work for a short period, but eventually, all of them seemingly fail to bring big profit. Ultimately, the ratio between the money bet and the money won will keep getting closer until players lose more than they win.
The primary reason betting systems are conclusively unsuccessful for some online casino games is that the outcome of games such as roulette or craps is 100 percent random and cannot be controlled. No system can successfully calculate or predict the outcome. Every spin and every roll of the dice is independent and does not follow any rules or standards. As Albert Einstein once said, “No one can possibly win at roulette unless he steals money off the table while the croupier isn’t looking.” Nonetheless, as a website that covers all angles and all topics, we have decided to discuss several different betting systems and ideas concerning it. We’ve included various experiments and data presenting the inevitable; the house will always have the edge. The “edge” can also be referred to as the casino or house advantage. Currently, there is no betting system that has proven otherwise.
Gambler’s Fallacy
One of the biggest myths in gambling is that if a win hasn’t occurred recently, it means that it has a bigger chance to take place because it will be overdue. This idea is known as “Gambler’s Fallacy.” Many gamblers have laid out betting systems dependent on Gambler’s Fallacy by placing bets against the recent outcomes of the game. For example, if the roulette ball keeps landing on black, they will bet on red. Many people tend to sell guaranteed betting systems based on Gamblers’ Fallacy, and they claim they will help you get rich quick. Even if you win once or twice, this is certainly not guaranteed to continue. If you still believe in Gambler’s Fallacy, here are some sources that have commented about it:
Encyclopedia Britannica (Under Gambling):
Gamblers’ Fallacy, also known as the Monte Carlo Fallacy, wrongly assumes that the different plays in a luck-based game are connected and that they are not independent of each other. Many betting systems were invented based on this Fallacy. To prove they do not work, casinos welcome any bets that are based on such betting systems because they know it does not give players an advantage.
The Theory of Gambling and Statistical Logic (by Richard A. Epstein):
There are a great number of betting systems that claim to be guaranteed, and there are a lot of people who believe in them. The fact is that betting systems are just one of the delusions in the history of gambling.
The Martingale Wagering System
The Martingale betting system follows the well-known concept of “Double or Nothing.” In this system, players will double up their wagers after suffering a loss. The Martingale system is designed to be used in games that offer even money bets (pays 1:1): for example, red and black bets in roulette or the Pass and Do Not Pass line bets at Craps. The theory is that if you lose and keep doubling up when you win, you will make up for all that you have lost + 1 extra unit. For instance, if you start with 1 dollar, and you lose 4 times in a row and win on the 5th time, it means you have bet a total of $15 and lost and on the 5th, you will bet $16 and you will win $16, so you made up for the losses and made a profit of one dollar. This betting system has two main flaws. The first one is that you can quickly lose all of the money before getting the chance to win. The second one is that you could reach the house limit (maximum bet) which will mean you cannot double up anymore.
Experiment Number 1:
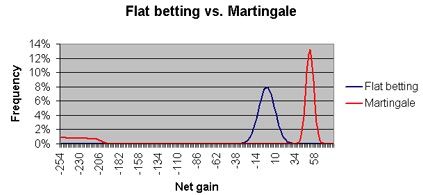
To prove the point, you can do a comparison experiment between flat betting and the Martingale system. Let’s say we will try it at the pass line bet in craps, a bet that has a 39.29 percent chance of winning. The player following the Martingale system will start with a bet of one dollar, and he will begin this trial with $255 as it is enough money to cover eight consecutive losses. The flat betting player will bet one dollar every single time, while the Martingale player will play 100 rounds or until he can’t cover the next bet. In such a case, he will have to leave the table with what he has left. In the event of the flat betting player, he will play one-hundred bets every single time. If you used a program to repeat the experience one million times for the two systems and charted the results, you will see a graph that looks like this one.
The Conclusion:
It is apparent from the chart that the flat betting player forms a bell-shaped curve that has a peak at the one dollar loss & he never strays away from this peak. On the other hand, the Martingale player shows a profit that is also indicated by the bell-shaped curve (on the right), which peaks at 51 dollars. However, on many occasions, we can see on the left that the player could not cover his bet and left the table after suffering many losses. This happened 19.56 percent of the time.
In the experiment, the loss session for the flat betting player was equal to $1.12 while it was $4.20 for the Martingale player. In these two cases, the ratio in terms of the money they lost to the money they’ve won was almost equal to 7/495. This is equal to the edge for the house of the pass line wager in craps. This is not a coincidence; in fact, this proves that no matter what betting system players use, the result will be equal or pretty close to the edge of the house. This is how casinos make a living.
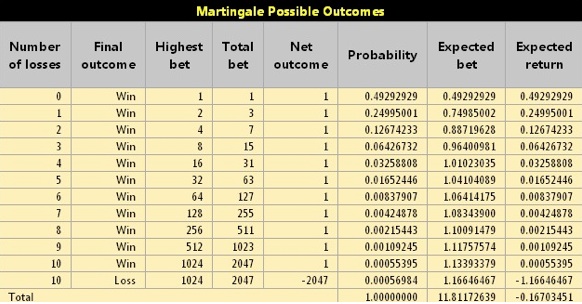
To prove the point even further, let’s take the Martingale player who wants to win one dollar and starts betting the same value. With a total bankroll of $2,047, the bettor can cover up to 10 consecutive losses. The following table will show all of the possible outcomes on every expected bet, probability & return:
The expected wager is the result of the probability and the total wager. In the same way, the expected return is also the result of the probability and the total return. The last row at the bottom shows the Martingale player had a total average wager of $11.81172639 and that his average loss was equal at $0.16703451. If we divide the average bet yield and the average loss, we get $0.01414141, which is the same number we will get if we divide the edge of the house for that bet at craps, which is 7/495. This shows that this system is neither worse nor better than the flat betting system as they all end with the same result, which is the house advantage.
Experiment Number 2:
This is yet another experiment that will prove the same point as the first experiment did. This one is based on a roulette betting system and tests three different types. Player 1 is going to use a flat bet that is equal to $1 each round. Player 2 will start betting $1, and he will begin to increase his bet by another $1 when he wins. If he loses, that will end his trial, and he will start betting with $1 again. Player 3 will begin with a bet of $1, and he will use the Martingale system, which means that he will double his bet when he loses. If he wins, his trial will end, and he will start another trial with a starting bet of $1. To make things realistic, the maximum bet for Player 3 is equal to $200. Here are the experiment’s results:
Player Number One:
– The total amount of money wagered is equal to $1,000,000,000
– Total losses is equal to $52,667,912
– The average wager is equal to $1
– The ratio between the losses and the wagered money is equal to 0.052668
– Expected loss is equal to $52,631,579
Player Number Two:
– The total amount of money wagered is equal to $1,899,943,349
– Total losses is equal to $100,056,549
– The average wager is equal to $1.90
– The ratio between the losses and the wagered money is equal to 0.052663
– Expected loss is equal to $99,997,018
Player Number Three:
– The total amount of money wagered is equal to $5,744,751,450
– Total losses is equal to $302,679,372
– The average wager is $5.74
– The ratio between the losses and the wagered money is equal to 0.052688
– Expected loss is equal to $302,355,340
The Conclusion:
It is clear the ratio between the money players lost to the amount they wagered is almost equal to the house advantage of 1/19, or 0.052632. This indicates the different betting systems will all end up with the same ratio. In the end, it does not matter what system you use, you will still end up with the house advantage.
The Ugly Truth Behind Betting Systems
The sad truth is, there is no successful betting system. If there was one, why would people be selling it instead of racking up millions by using it at casinos themselves? The online realm is filled with people who are trying to sell these wagering systems and ones making promises that it can beat the casinos at luck-based games. These people are the same as the snake oil salesmen in the nineteenth century. You should not, under any circumstances, waste your money on these systems because every time they are put on a computer trial, they will fail and they will show a ratio of money wagered to money lost that equals flat betting and the house advantage of the given game.
If you try to ask the sales representative why the computer trials fail miserably, he will reply by saying that no one plays millions and billions of trials at the casino. He will also claim that such a betting system works fine well in life, and it fails when it is pitted against a computer simulation. This is an amusing response because computer simulations and trials are used in every single field. Professionals and researchers of all types rely on them, but apparently, not if it is testing wagering systems. If it does not succeed on a virtual simulation, then it will not work in real life; this is why they call it a test.
These gambling systems and the people selling them have been here since gambling was invented, and none of them were ever proven to be successful. This is a nasty business as these salesmen switch from one system to the next. They are always rehashing old systems and trying to pawn them off as new ones to make a quick buck by scamming people.
The salesmen of these systems usually promise players ridiculous advantages. If these advantages were definite they wouldn’t need to sell these systems for a living because they could make millions and millions by using it at the casinos themselves. For example, if a system promises an advantage as small as 1 percent on bets that pay 1:1, it means it will be very easy for you to turn $100 into $1,000,000. To prove this here is the computer simulation of 4 different tests. Two of them simulate the 1 percent advantage with a bankroll of $100 and the other of $1000 while the two other tests present the 2 percent advantage with the same bankrolls. Here are the four different results of the four cases:
1% Advantage -$100 Bankroll
– The amount of wagers won is equal to 7,182,811,698, which is equal to 50.4999 percent.
– The amount of wagers lost is equal to 7,040,599,544, which is equal to 49.5001 percent.
– Players lost their bankroll before achieving $1,000,000: 16,249, which equals to 16.981 percent.
– The number of players who achieved the $1,000,000 equals 79,438, which is equal to 83.019 percent.
– The number of rounds to achieve the $1,000,000 equals to 174,972.
2 % Advantage – $100 Bankroll
– The amount of wagers won is equal to 7,027,117,205, which is equal to 51 percent.
– The amount of wagers lost is equal to 6,751,539,769, which equals to 49 percent.
– Players lost their bankroll before achieving $1,000,000: 4,180, which is equal to 1.901 percent.
– The number of players who achieved the $1,000,000 equals 215,702, which is equal to 98.099 percent.
– The number of rounds to achieve the $1,000,000 is equal to 63,775.
1% Advantage – $1000 Bankroll
– The amount of wagers won is equal to 5,213,026,190 which is equal to 50.4999 percent.
– The amount of wagers lost is equal to 5,109,817,544, which is equal to 49.5001 percent.
– Players lost their bankroll before achieving 1,000,000: 734, which equals to 0.9715 percent.
– The number of players who reached $1,000,000 is equal to 74,818, which converts to 99.0285 percent.
– The number of rounds to achieve $1,000,000 is equal to 137,208.
2% Advantage – $1000 Bankroll
– The amount of wagers won is 6,332,837,070, which converts to 50.9996 percent.
– The amount of wagers lost is equal to 6,084,596,671, which converts to 49.004 percent.
– Players lost their bankroll before achieving $1,000,000: 1, which converts to 0.0004 percent.
– The number of players who achieved $1,000,000 is 267,445, which converts to 99.9996 percent.
– The number of rounds to achieve $1,000,000 is equal to 46,428.
This shows that with a bankroll as small as $100 and an advantage of 1 percent, players can quickly grind their way to $1,000,000. If that were true, we would all be millionaires and casinos would go out of business.
There are also many people online who are selling gambling schemes and claim these schemes aren’t a betting system. They will use big fancy words such as Fractals and Chaos, but they will not provide you with anything useful.
The Conclusion:
If you want to win at any online casino, play smart, manage your money and maybe you will get lucky and hit the jackpot at slots or get a big win at the roulette table. You can also achieve considerable winnings in games that do not rely on pure luck, such as poker or blackjack. Whatever it is you do, do not rely on a betting system that promises riches and fortune because it will never do as promised. You will end up wasting your money buying it and wasting more money following it.